Как посчитать средний возраст сотрудников формула

Опубликовано: 07.05.2025

• Как определить средний возраст сотрудников
  
• Как считать среднюю численность
  
• Как рассчитать численность
  
• Как определить среднесписочную численность
  
• Как рассчитать среднесписочную численность работников
  
• Как определить численность трудовых ресурсов
  
• Как рассчитать среднегодовую численность работников
  
• Как рассчитать количество персонала
  
• Как вычислить среднесписочную численность
  
• Как рассчитать средний заработок
  
• Как посчитать среднесписочную численность
  
• Как считать среднее в 2017 году
  
• Как считать среднесписочную численность работников
  
• Как учесть средний заработок в 2017 году
  
• Как минздрав считает среднюю зарплату врачей
  
• Как определить среднюю заработную плату
  
• Как рассчитать количество работников
  
• Как рассчитать норматив численности
  
• Как рассчитать среднемесячный доход
  
• Как рассчитать среднее число
  

Качественная HR-аналитика является опорой для анализа ситуации и принятия решений в сфере управления персоналом.

Оглавление

Качественная HR-аналитика является опорой для анализа ситуации и принятия решений в сфере управления персоналом.

Основные задачи которые может решить HR-аналитика:

• Предоставлять реальную статистику и аналитику по персоналу для принятия решений.
• Анализировать и увеличивать эффективность: персонала, процессов, методов и инструментов работы.
• Находить эффективные и экономичные модели принятия решений.
• Организовать эффективный контроль персонала
• Прогнозировать проблемы в будущем
• Выявлять скрытые закономерности.

Статистика по зарубежным компаниям утверждает, что эффект от внедрения системы оценки HR-службы покрывает расходы и издержки от ее реализации. Процедура оценки помогает менеджерам выявить и скорректировать слабые места в области управления персоналом, а также сфокусировать деятельность HR-службы на важных вопросах.

Основные варианты применения HR аналитики в компании:

1. Реальные HR показатели

Руководители компаний обязаны опираться на цифры и регулярно сравнивать себя с конкурентами.

Без HR-метрик практически невозможно доказать руководству, что такой-то показатель «нормальный» или же находиться на критическом уровне.

Формирование адекватных ожиданий у руководства от HR подразделений.

2. Планирование бюджета

HR-метрики позволяют содержательно проработать многие вопросы, связанные с бюджетом:

• доказать целесообразность расходов в HR-бюджете, обосновав показателями эффективности работы сотрудников;
• разработка целевых значений затрат на персонал, KPI и эффективности персонала;
• анализ завышенных или заниженных значения некоторых показателей могут быть отправной точкой для корректировки бюджета.

3. Выявление проблем

«Высокие» или «низкие» показатели — сигнал для дальнейшего детального изучения. Растущие расходы, снижающаяся эффективность, раздутый штат или отставание в области автоматизации — все это может быть важным сигналом.

4. Поиск лучших практик и совершенствование HR-процессов

HR-аналитика лучше всего решает задачу выявления основных областей отставания. Сопоставление HR-показателей вашей компании с рынком может служить отправной точкой для постановки целей всей HR службе.

5. Разработки KPI

На основании hr-аналитики разрабатываются KPI показатели HR-службы, а также обосновываются целевые значений показателей.

Измерить можно почти все HR-функции, в любом разрезе. Но измерение ради измерений не несет ни кокой пользы для компании. Получаемые данные необходимо анализировать и использовать при разработке политики управления персоналом.

Что именно необходимо измерять, зависит от того, какие цели стоят перед компанией. Тем HR- специалистам, кто только внедряет систему оценки эффективности, можно
порекомендовать начать с измерения наиболее понятных HR-функций: проанализировать
эффективность самой HR службы.

HR-аналитика — это умение использовать простейшие показатели для повышения эффективности работы персонала компании.

Результаты опроса применении HR-метрик в российских компаниях в 2016 г.

В HR-практике используются различные группы метрик:

• общие статистические данные, характеризующие находящиеся в распоряжении компании человеческие ресурсы;
• показатели, которыми оценивается качество человеческих ресурсов и эффективность их использования — метрики HR-эффективности;
• метрики для оценки эффективности деятельности отдельных сотрудников/ подразделений;
• метрики для оценки эффективности деятельности самой HR-службы.

Общие статистические данные HR аналитики:

Сегментация сотрудников возрасту, полу, стажу работы в компании, образовательно-квалификационному уровню.

1. Средний возраст сотрудников

Формула расчета:

Средний возраст работников по формуле расчета средней величины:

Х = (Х1 +Х2+Х3….+Хn) /С,

• Х – средний возраст работников организации;
• Х1, Х2,Х3… Хn – возраст каждого работника;
• С – количество работников в организации (списочная численность) на первое число месяца, следующего за отчетным периодом.

Частные варианты HR-метрики:

1. Средний возраст сотрудников по подразделениям.

2. Средний возраст сотрудников по половому признаку.

Почему показатель важен?
— увеличить эффективность рекрутинга;
— уменьшить конфликтность и напряженность в коллективе (разница поколений);
— Сбалансировать штат по эффективности (возрастные – опыт, молодые сотрудники –инновации, развитие);
— система оценки, мотивации и поощрения для «молодых» и более «возрастных» групп должна различатся.

2. Сегментация по половому признаку

Х = (Х /С, )*100%

где: — Х – количество сотрудников мужского пола (женского пола) ;
С – количество сотрудников в организации (списочная численность) на первое число месяца, следующего за отчетным периодом.

3. Средний стаж работы сотрудников в компании

Х = (Х1 +Х2+Х3….+Хn) /С,

где: — Х – средний стаж сотрудников организации;
— Х1, Х2,Х3… Хn – стаж каждого сотрудников на первое число месяца, следующего за отчетным периодом;
С – количество сотрудников в организации (списочная численность) на первое число месяца, следующего за отчетным периодом.

Показатель позволяет:

Средний стаж в компании сигнализирует о удовлетворенности условиями труда и лояльностью к компании.
— оценить конкуретноспособность системы вознаграждений и льгот;
— оценить эффективность мотивационных программ, программ грейдирования, программы карьерного развития, ротации и пр.;

4. Средний стаж сотрудника на момент увольнения

Х = (Х1 +Х2+Х3….+Хn) /С,

— Х – средний стаж сотрудников на дату увольнения организации;
— Х1, Х2,Х3… Хn – стаж каждого уволившегося работника на первое число месяца, следующего за отчетным периодом;
С – количество уволившихся сотрудников за отчетный период.

Показатель позволяет:

• можно оценить, когда сотрудник будет близок к увольнению.
• определить, когда запустить программу по удержанию ключевых сотрудников, провести ротацию, или подготовить кандидатов из кадрового резерва.
• оценить эффективность процессов удержания персонала (конкуретноспособность системы вознаграждений и льгот, мотивационные программы, программы грейдирования, программы карьерного развития и пр.);

5. Квалификационный уровень (Среднее, СПО, ВО) сотрудников

Кв = (Уо /С)*100%,

• Кв – процент сотрудников имеющий определенный уровень квалификации (образования);
• Уо – количество сотрудников имеющих определенный уровень квалификации (образования);
• С – количество работников в организации (списочная численность) на первое число месяца, следующего за отчетным периодом.

Позволяет определить:

• количество сотрудников имеющих средним полным образование (11 кл.);
• количество сотрудников имеющих средне — профессиональное образование (техникум, колледж);
• количество сотрудников имеющих высшие образование.
• уровень образования (квалификации) человеческого капитала.

Показатели эффективности HR-службы

6. Выполнение плана HR службы

К=(Зусп: З)*100 %,

Зусп – количество успешно выполненных задач;
З — общее количества задач по плану;

Позволяет определить:

1. Эффективность выполнения плана: соблюдение временных рамок, достижение установленных целей и результатов.
2. Адекватность и достижимость поставленных целей и показателей.
3. Выявление проблем в работе HR службы и их корректировка.

7. Бюджет HR службы и его структура

Выполнение бюджета (ВБ) – рассчитывается по формуле:

ВБ = (Σ ФЗ : Σ ЗЗ) х 100 (%),

Σ ФЗ – сумма фактических затрат за отчетный период;
Σ ЗЗ – сумма запланированных затрат в HR-бюджете за отчетный период.

В частности рассчитывается показатель по каждой строке в бюджете.

ВБ(строка) = Σ ФЗ : Σ ЗЗ х 100 (%),

Σ ФЗ – сумма фактических затрат по строке бюджета за отчетный период;
Σ ЗЗ – сумма запланированных затрат по строке бюджета за отчетный период.

Важные параметры структуры бюджета:

• Затраты на подбор персонала как % от HR-бюджета.
• Затраты на обучение как % от HR-бюджета.
• Затраты на адаптацию как % от HR-бюджета.
• Затраты на проведение корпоративных мероприятий как % HR-бюджета.
• Затраты на внешних провайдеров как % HR-бюджета.

Результаты опроса о структуре HR-бюджета российских компаний в 2016 г.

8. Текучесть персонала/ Уровень текучести персонала

Уровень текучести персонала в организации представляет собой процент сотрудников, покинувших организацию (по разным причинам) в течение определённого периода.

Т=(Ку:С)*100 (%),

Ку — количество уволенных работников за период;
С- среднесписочная численность штатных работников.

Частные варианты HR-метрики:

1. Текучесть персонала за период.

2. Текучесть персонала в период адаптации. (3-6 месяцев).

Высокие показатели увольнений в в период адаптации указывают на ошибки в подборе персонала (критерии отбора, соответствие кандидатов) и его адаптации (процесс адаптации, наличие систем наставничества и пр.), несоответствие внутренних мотивов и корпоративной культуры, отношения с руководством.

3. Текучесть персонала в течение 1 года после найма.

Высокие показатели увольнений в течение 1 года работы указывают на ошибки в подборе персонала (критерии отбора, эффективность рекрутеров) и его адаптации (процесс адаптации, наличие систем наставничества и пр.), отношения с руководством.

4. Текучесть персонала по подразделениям.

По разным подразделениям компании будут разные допустимые уровни текучести.
Текучесть персонала стоит контролировать регулярно — проводить анализ каждые квартал, каждые полгода или каждый год.

Показатель позволяет:

• оценить издержки от потерь персонала и их целесообразность;
• оценить эффективность процессов удержания персонала (конкуретноспособность системы вознаграждений и льгот, мотивационные программы, программы грейдирования, программы карьерного развития и пр.);
• планировать численность и затраты на функции (бюджетирование затрат);
• планировать объемы необходимых ресурсов в области адаптации, обучения и развития персонала;
• выявить проблемы в управлении эффективностью персонала.
• Мотивы ухода сотрудников.

О чем говорят высокие / низкие значения?

Низкие абсолютные показатели текучести персонала (до 5% в год) в большинстве случаев способствуют своевременному обновлению коллектива и не требует оперативного вмешательства в процесс. Небольшой коэффициент текучести даже полезен для организации, так как происходит обновление состава организации (привносится новые практики, свежий взгляд и т.д.).

Если же у компании текучесть персонала близка к 0% или значительно ниже медианы рынка в сопоставимой отрасли, то возможно, стоит уделить внимание качественным характеристикам кадрового состава (структуру персонала в разбивке по возрасту, стажу, квалификации и пр.) и эффективности работников. Возможные риски:

• снижение эффективности работников (неэффективные не увольняются);
• технологическое отставание (нет притока новых идей и технологий + сотрудники не востребованы на рынке труда);
• «синхронное старение» и волнообразный уход сотрудников без наличия адекватной замены;
• раздувание фонда оплаты труда.

Cредний (допустимый) уровень текучести персонала обычно (без учета отраслевой специфики) составляет от 5 до 10%. При этом, неизбежно возрастают расходы по подбору и адаптации персонала, снижается производительность труда и возникают связанные с ними потери.

Высокий уровень текучести персонала (без учета отраслевой специфики) от 10 до 30 % может указывать на то, что компания либо неспособна контролировать потерю ключевых сотрудников, либо характеризовать стратегию удержания персонала. В первом случае, это тревожный сигнал, который ведет к дестабилизации развития компании.

Если показатель значительно выше или значительно ниже уровня по отрасли, необходимо провести дополнительный анализ причин увольнений.

Увеличение естественной текучести персонала по отношению к общему объему увольнений может говорить о проблемах в стратегии управления персоналом (в области определения размера и состава вознаграждения, системе мотивации и льгот, возможностях обучения и карьерного развития, ценностном предложения работодателя и пр.)

Результаты опроса о текучести в российских компаний в 2016 г.

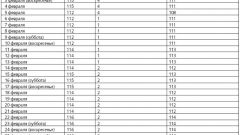
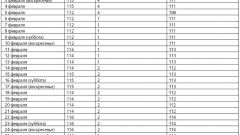
На заводе, где число рабочих составляет 1000 человек, было проведено выборочное обследование возраста рабочих. Методом случайного бесповторного отбора было отобрано 50 человек. Результаты обследования следующие:

Возраст рабочих (лет)	до 30	30 – 40	40 – 50	50 – 60	свыше 60
Число рабочих	8	22	10	6	4

С вероятностью 0,997 определите предел, в котором находится средний возраст рабочих завода.

Решение:

1. Рассчитаем средний возраст рабочих завода в выборочной совокупности. Все расчёты оформим в таблицу.

Возраст рабочих (лет)	Число рабочих (f)	Среднее значение интервала (х)
до 30	8	25	200	-15,2	231,04	1848,3
30 – 40	22	35	770	-5,2	27,04	594,88
40 – 50	10	45	450	4,8	23,04	230,4
50 – 60	6	55	330	14,8	219,04	1314,2
свыше 60	4	65	260	24,8	615,04	2460,2
Итого:	50	-	2010	-	-	6448

Средняя выборочная в данном случае будет рассчитываться по формуле средней арифметической взвешенной:

2. Рассчитаем дисперсию выборочной совокупности:

3. Средняя ошибка выборки составит:

4. С вероятностью 0,997 рассчитаем предельную ошибку выборочной средней.

t - коэффициент доверия.

Значение коэффициента доверия t определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного наблюдения и берётся из готовых таблиц.

Наиболее часто встречающиеся в задачах подобного рода значения t:

Вероятность Р	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

При Р = 0,997, t = 3.

Δ = 1,565 * 3 = 4,696 лет.

5. Определим пределы, в которых находится средний возраст рабочих завода.

Генеральная средняя ( ) находится в пределах

40,2 - 4,696 ˂ ˂ 40,2 + 4,696.

35,5 ˂ ˂ 44,9

С вероятностью 0,997 можно утверждать, что средний возраст рабочих завода находится в пределах 35,5 ˂ ˂ 44,9 лет.

Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.

Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности.

Вычисление среднего – один из распространенных приемов обобщения; средний показатель отрицает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей.

Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов.

Остановимся на некоторых общих принципах применения средних величин.
1. Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц.
2. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц.
3. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.
4. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.

5.2. Виды средних и способы их вычисления

Рассмотрим теперь виды средних величин, особенности их исчисления и области применения. Средние величины делятся на два больших класса: степенные средние, структурные средние.

К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.

В качестве структурных средних рассматриваются мода и медиана.

Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:

где X_i – варианта (значение) осредняемого признака;
m – показатель степени средней;
n – число вариант.

Взвешенная средняя считается по сгруппированным данным и имеет общий вид

где X_i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m – показатель степени средней;
f_i – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.

Приведем в качестве примера расчет среднего возраста студентов в группе из 20 человек:

№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)	№ п/п	Возраст (лет)
1 2 3 4 5	18 18 19 20 19	6 7 8 9 10	20 19 19 19 20	11 12 13 14 15	22 19 19 20 20	16 17 18 19 20	21 19 19 19 19

Средний возраст рассчитаем по формуле простой средней:

Сгруппируем исходные данные. Получим следующий ряд распределения:

Возраст, Х лет	18	19	20	21	22	Всего
Число студентов	2	11	5	1	1	20

В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте Х лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:

Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
средняя гармоническая, если m = -1;
средняя геометрическая, если m –> 0;
средняя арифметическая, если m = 1;
средняя квадратическая, если m = 2;
средняя кубическая, если m = 3.

Формулы степенных средних приведены в табл. 4.4.

Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:

В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.

Виды степенных средних

Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.

Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым [1] . Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины. Покажем это правило на примере средней геометрической.

Формула средней геометрической

используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики.

Приняв q_n в качестве определяющего показателя и заменяя индивидуальные значения показателей динамики средними, приходим к соотношению

5.3. Структурные средние

Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).

В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.

Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в каком-то из интервалов признака X. С помощью интерполяции в этом медианном интервале находят значение медианы:

где X_Me – нижняя граница медианного интервала;
h_Me – его величина;
(Sum m)/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
S_Me-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
m_Me – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).

В нашем примере могут быть получены даже три медианных значения – исходя из признаков количества предприятий, объема продукции и общей суммы затрат на производство:

Таким образом, у половины предприятий уровень себестоимость единицы продукции превышает 125,19 тыс. руб., половина всего объема продукции производится с уровнем затрат на изделие больше 124,79 тыс. руб. и 50 % общей суммы затрат образуется при уровне себестоимости одного изделия выше 125,07 тыс. руб. Заметим также, что наблюдается некоторая тенденция к росту себестоимости, так как Ме₂ = 124,79 тыс. руб., а средний уровень равен 123,15 тыс. руб.

При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Для интервального ряда с равными интервалами величина моды определяется как

где Х_Mo – нижнее значение модального интервала;
m_Mo – число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
m_Mo-1 – то же для интервала, предшествующего модальному;
m_Mo+1 – то же для интервала, следующего за модальным;
h – величина интервала изменения признака в группах.

Для нашего примера можно рассчитать три модальных значения исходя из признаков числа предприятий, объема продукции и суммы затрат. Во всех трех случаях модальный интервал один и тот же, так как для одного и того же интервала оказываются наибольшими и число предприятий, и объем продукции, и общая сумма затрат на производство:

Таким образом, чаще всего встречаются предприятия с уровнем себестоимости 126,75 тыс. руб., чаще всего выпускается продукция с уровнем затрат 126,69 тыс. руб., и чаще всего затраты на производство объясняются уровнем себестоимости в 123,73 тыс. руб.

5.4. Показатели вариации

Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.

Для измерения вариации в статистике применяют несколько способов.

Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным (X_max ) и минимальным (X_min) наблюдаемыми значениями признака:

Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.

Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:

При повторяемости отдельных значений Х используют формулу средней арифметической взвешенной:

(Напомним, что алгебраическая сумма отклонений от среднего уровня равна нулю.)

Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.

Дисперсия признака (s 2 ) определяется на основе квадратической степенной средней:

Показатель s, равный , называется средним квадратическим отклонением.

В общей теории статистики показатель дисперсии является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой дисперсии в математической статистике, что позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов.

Обычно уже при n > (15÷20) расхождение смещенной и несмещенной оценок становится несущественным. По этой же причине обычно не учитывают смещенность и в формуле сложения дисперсий.

Если из генеральной совокупности сделать несколько выборок и каждый раз при этом определять среднее значение признака, то возникает задача оценки колеблемости средних. Оценить дисперсию среднего значения можно и на основе всего одного выборочного наблюдения по формуле

где n – объем выборки; s 2 – дисперсия признака, рассчитанная по данным выборки.

Величина носит название средней ошибки выборки и является характеристикой отклонения выборочного среднего значения признака Х от его истинной средней величины. Показатель средней ошибки используется при оценке достоверности результатов выборочного наблюдения.

Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.

1. Коэффициентом осцилляции отражает относительную колеблемость крайних значений признака вокруг средней

2. Относительное линейное отключение характеризует долю усредненного значения признака абсолютных отклонений от средней величины

3. Коэффициент вариации:

является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.

У такого способа оценки вариации есть и существенный недостаток. Действительно, пусть, например, исходная совокупность рабочих, имеющих средний стаж 15 лет, со средним квадратическим отклонением s = 10 лет, «состарилась» еще на 15 лет. Теперь = 30 лет, а среднеквадратическое отклонение по-прежнему равно 10. Совокупность, ранее бывшая неоднородной (10/15 × 100 = 66,7%), со временем оказывается, таким образом, вполне однородной (10/30 × 100 = 33,3 %).

[1] Боярский А.Я. Теоретические исследования по статистике: Сб. Науч. Трудов.– М.: Статистика,1974. С. 19–57.

Например, у вас есть список студентов с указанием дней рождения и возраста в Excel, как вы можете рассчитать средний возраст по заданному месяцу или году? А что, если в Excel вычислить среднее значение по определенной дате? В этой статье мы расскажем о нескольких приемах, которые помогут легко их решить в Excel.

• Вычислить среднее значение за год / месяц с помощью формул массива в Excel
• Рассчитайте среднее значение за год / месяц с помощью команды фильтра в Excel
• Рассчитать среднее по дате в Excel
• Пакетный расчет среднего возраста по годам или месяцам в Excel

Вычислить среднее значение за год / месяц с помощью формул массива в Excel

Например, у вас есть таблица, показанная на следующем снимке экрана. Вы можете быстро рассчитать средний возраст по годам или месяцам с помощью формул массива в Excel.

Средний возраст по месяцам : Выберите пустую ячейку помимо таблицы, например Ячейку F2, введите формулу =SUM((MONTH(B2:B15)=12)*C2:C15)/SUM(IF(MONTH(B2:B15)=12,1)) в него и нажмите Ctrl + Shift + Enter одновременно.

Внимание: В этой формуле B2: B15 - это столбец «День рождения», C2: C15 - это столбец «Возраст», 12 - это указанный месяц «декабрь», по которому вы будете усреднять, и вы можете изменить его в зависимости от ваших потребностей.

Средний возраст по годам : Выберите пустую ячейку помимо таблицы, говорит Ячейка F4, введите формулу =SUM((YEAR(B2:B15)=1990)*C2:C15)/SUM(IF(YEAR(B2:B15)=1990,1)) в него и нажмите Ctrl + Shift + Enter одновременно.

Примечание: В этой формуле B2: B15 - это столбец дня рождения, C2: C15 - столбец возраста, 1990 - это конкретный год, по которому вы хотите усреднить, и вы можете изменить их в зависимости от ваших потребностей.

Формула слишком сложна для запоминания? Сохраните формулу как запись Auto Text для повторного использования одним щелчком мыши в будущем! Подробнее . Бесплатная пробная версия

Легко рассчитывать возраст по заданным датам рождения (дням рождения) в Excel

Kutools for Excel's собирает множество часто используемых формул для пользователей Excel, чтобы легко вычислять, не запоминая формулы, включая Рассчитать возраст по рождениюy Формула. Полнофункциональная бесплатная 30-дневная пробная версия!

Рассчитайте среднее значение за год / месяц с помощью команды фильтра в Excel

В нашем примере таблицы, показанной на следующем снимке экрана, мы также можем сначала отфильтровать столбец дня рождения, а затем вычислить среднее значение по году или месяцу после фильтрации с помощью функции промежуточных итогов в Excel.

1. Выберите столбец дня рождения и щелкните значок Данные > Фильтр.

2. Нажмите рядом с заголовком столбца столбца "День рождения", а затем в раскрывающемся списке нажмите кнопку Фильтры даты > Все даты периода > сентябрь (или любой другой месяц, по которому вы хотите усреднить). См. Снимок экрана ниже:

Внимание: Если вы хотите усреднить возраст по конкретному году, вам нужно нажать на рядом с заголовком столбца столбца "День рождения", а затем снимите отметку со всех лет, кроме года, по которому будет производиться среднее значение, и нажмите OK кнопка. См. Снимок экрана ниже:

3. Теперь возраст фильтруется по конкретному году или месяцу. Выберите любую пустую ячейку, говорит Ячейка C42, формула = ПРОМЕЖУТОЧНЫЙ ИТОГ (1; C3: C9) (C3: C9 означает все отфильтрованные возрасты в столбце Возраст) и нажмите Enter ключ.

Рассчитать среднее по дате в Excel

Иногда вам может потребоваться вычислить среднее значение на заданную дату. Например, у вас есть таблица, показанная на следующем экране, и вам нужно рассчитать среднее значение Amount, полученное за 2014-04-04, вы можете решить это следующим образом:

Выберите пустую ячейку, введите формулу =AVERAGEIF(J2:J24,P2,M2:M24) в него и нажмите Enter ключ. Тогда вы получите среднее значение указанной даты.

Внимание: В формуле = СРЗНАЧЕСЛИ (J2: J24, P2, M2: M24), J2: J24 - это столбец даты, P2 - это ссылочная ячейка с датой, по которой вы будете усреднять, M2: M24 - это столбец суммы, в котором вы рассчитаете среднее , и вы можете изменить их в зависимости от ваших потребностей.

Пакетный расчет среднего возраста по годам или месяцам в Excel

Если вам нужно рассчитать средний возраст каждого месяца (с января по декабрь) или каждого года в Excel, применение сложной формулы массива может занять много времени. Здесь я расскажу о надстройке третьей части Kutools for Excel, чтобы решить эту проблему.

Kutools for Excel - Включает более 300 удобных инструментов для Excel. Полнофункциональная бесплатная 30-дневная пробная версия, кредитная карта не требуется! Get It Now

1. Выберите столбец даты, по которому вы будете рассчитывать среднее значение, и щелкните значок Kutools > Формат > Применить форматирование даты.

2. В открывшемся диалоговом окне «Применить форматирование даты» выберите форматирование даты, в котором отображается только название месяца. Форматирование даты коробка, например " Вт "Или" Март "и щелкните Ok кнопка. Смотрите скриншот:

Чаевые: Если вам нужно рассчитать средний возраст по годам, выберите формат даты, показывающий только год (например, «2001») в Форматирование даты коробка.

Применить форматирование даты - одна из утилит Kutools for Excel, которая может помочь вам изменить массовые даты на определенное форматирование даты, соответствующее разным клиентам и разным странам в Excel.

Kutools for Excel - Включает более 300 удобных инструментов для Excel. Полнофункциональная бесплатная 30-дневная пробная версия, кредитная карта не требуется! Get It Now

3. Продолжайте выбирать столбец даты и щелкните Kutools > К фактическому. Эта утилита преобразует дату в текст названия месяца.

К фактическому является одной из утилит Kutools for Excel, и она может помочь вам заменить фактическое значение (отображаемое в строке формул, например формула = A1 + B1 ) с отображаемым значением (которое вы видите в выбранной ячейке, например, результат формулы 10 ). Полнофункциональная бесплатная 30-дневная пробная версия!

4. Выберите диапазон, в котором вы будете усреднять по месяцам / годам, и нажмите кнопку Kutools > Content > Расширенные ряды комбинирования.

Расширенные ряды комбинирования является одной из утилит Kutools for Excel, и она может помочь вам объединить / объединить строки на основе одного и того же значения в одном столбце, а затем выполнить некоторые вычисления для других столбцов, таких как сумма, количество, среднее, максимальное и т. д. Полнофункциональная бесплатная 30-дневная пробная версия!

5. В открывшемся диалоговом окне «Объединить строки на основе столбца» укажите параметры, как показано на скриншоте выше:

1. Щелкните столбец Имя, а затем щелкните значок Сочетать > Запятая;
2. Щелкните столбец День рождения, а затем щелкните значок Основной ключ.
3. Щелкните столбец Возраст, а затем щелкните значок Рассчитать > Средняя.

6, Нажмите Ok кнопка. Затем вы увидите, что средний возраст каждого месяца рассчитывается с перечислением соответствующих имен. См. Снимок экрана ниже:

Kutools for Excel - Включает более 300 удобных инструментов для Excel. Полнофункциональная бесплатная 30-дневная пробная версия, кредитная карта не требуется! Get It Now

Читайте также:

  
• Как прописать в должностной инструкции наставничество
  
• Как перевести директор компании
  
• Кто имеет право на сокращенный рабочий день
  
• Какая зарплата в колхозе
  
• Как заполнить служебную записку на командировку