Пенсионер начинает прогулку в точке a найдите вероятность того что он придет в точку

Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку F.

Решение задачи

В данном уроке показывается пример решения задачи с применением теории вероятностей. Для успешного решения задачи необходимо знать, что вероятность — это степень возможности наступления некоторого события, или отношение числа благоприятствующих исходов к общему числу возможных исходов. Таким образом, решение задачи сводится к применению формулы теории вероятностей: , где -благоприятное число исходов, а — общее число исходов. Решение задачи разбивается на этапа. Сначала определяется вероятность того, что пенсионер начнет прогулку именно с дорожки , при этом Затем выполняется вычисление вероятности того, что прогулка будет продолжена по маршруту , при этом По теореме умножения вероятностей: вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место. Таким образом, результат вычисления произведения и является искомым ответом.

Эта задача аналогична задачам вида В6, поэтому ее с успехом можно использовать в качестве подготовки к ЕГЭ по математике.

Основы
теории
вероятностей
Чикрин Евгений
Александрович
КАЗАНЬ2016

Примеры непосредственного
определения вероятностей
ЗАДАЧА 1.
На семинар приехали 3 ученых из
Норвегии, 3 из России и 4 из Испании. Порядок
докладов определяется жеребьёвкой. Найдите
вероятность того, что восьмым окажется доклад
ученого из России.
Решение.
Число благоприятных исходов m=3,

вероятность
ОТВЕТ: 0,3

Примеры непосредственного определения вероятностей

ЗАДАЧА 4. Вероятность того, что чайник прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите

ЗАДАЧА 5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Веро

Основные правила вычисления вероятностей сложных событий

ЗАДАЧА 9. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Пенсионер н

Основные правила вычисления вероятностей сложных событий

Формула полной вероятности

Повторение испытаний. Формула Бернулли

ЗАДАЧА 14. За один выстрел стрелок поражает мишень с вероятностью 0,1. Найдите вероятность того, что при пяти выстрелах он хотя бы раз попадет

Таксист за месяц проехал 5500 км. Стоимость 1 л бензина 32 рубля. Средний расход бензина на 100 км составляет 9 л. Сколько рублей потратил таксист на бензин за этот месяц?

Задание 1. Вариант 240 Ларина. ЕГЭ 2019 по математике.

На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4го класса по математике в 2007 году по 100500 – бальной шкале. По данным диаграммы найдите число стран, в которых средний балл заключен между 495 и 515.

Задание 2. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Площадь треугольника АВС равна 28. DE – средняя линия. Найдите площадь трапеции ABDE.

Решение

Задание 3. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно и не проходя дважды по одной и той же дорожке. Схема дорожек показана на рисунке. Найти вероятность того, что Павел Иванович попадет в точку G. Результат округлите до сотых.

Решение

Задание 4. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 5. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Угол АСО равен 620. Его сторона СА касается окружности с центром в точке О. Отрезок СО пересекает окружность в точке В. Найдите градусную меру дуги АВ окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Решение

Задание 6. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Функция y=f(x) определена на интервале (-5;6). На рисунке изображен график функции y=f(x) . Найдите среди точек x 1 ,x 2 . x 7 те точки, в которых производная функции y=f(x) равна нулю. В ответ запишите количество найденных точек.

Решение

Задание 7. Вариант 240 Ларина. ЕГЭ 2019 по математике.

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми ВА 1 и АС. Ответ дайте в градусах.

Решение

Задание 8. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите значение выражения при a=216

Задание 9. Вариант 240 Ларина. ЕГЭ 2019 по математике.

На верфи инженеры проектируют новый аппарат для погружения на большие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выраженная в ньютонах, будет определяться по формуле F A =apgr 3 , где a=4.2 - постоянная, r - радиус аппарата в метрах, p=1000 кг/м 3 – плотность воды, а g - ускорение свободного падения (считайте g=10 Н/кг). Каков может быть максимальных радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 14 406 000 Н? Ответ дайте в метрах.

Задание 10. Вариант 240 Ларина. ЕГЭ 2019 по математике.

За первый час автомобиль проехал 100 км, следующие два часа он ехал со скоростью 90 км/ч, затем автомобиль сломался. Через час приехал эвакуатор и за шесть часов отвез его обратно к месту оправления. Найдите среднюю скорость автомобиля за все время путешествия.

Задание 11. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите наименьшее значение функции y=4cosx+13x+9 на отрезке

Задание 12. Вариант 240 Ларина. ЕГЭ 2019 по математике.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку [-2пи;-пи/2]

Задание 13. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Дана четырехугольная пирамида SABCD с вершиной S и прямоугольником ABCD в основании. Известно, что SA=SB=SC=SD=13, AD=BC=12, AB=CD=5. Из точки А на ребро SC опущен перпендикуляр АН. А) Докажите, что SH=CH Б) Найдите длину отрезка НК, где К - точка пересечения ребра SB плоскостью, проходящей через точку Н перпендикулярно ребру SB.

Задание 14. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 15. Вариант 240 Ларина. ЕГЭ 2019 по математике.

На диагонали LN параллелограмма KLMN отмены точки Р и Q, причем LP=PQ=QN А) Докажите, что прямые КР и KQ проходят через середины сторон параллелограмма. Б) Найдите отношение площади параллелограмма KLMN к площади пятиугольника MRPQS, где R - точка пересечения КР со стороной LM, S - точка пересечения KQ с MN

Задание 16. Вариант 240 Ларина. ЕГЭ 2019 по математике.

В июле планируется взять кредит в банке в размере S тыс. рублей (S - натуральное число) сроком на 3 года. Условия возврата кредита таковы: - каждый январь долг увеличивается на 22,5% по сравнению с концом предыдущего года; - в июне каждого года необходимо выплатить одним платежом часть долга; - в июле каждого года величина долга задается таблицей

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

Задание 17. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите все значения параметра a , при каждом из которых уравнение

имеет решения, и определите то решение, которое получается только при единственном значении параметра a .

Аристарх Луков‐Арбалетов совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие-в поле F или в болото M. Найдите вероятность того, что Аристарх забредет в болото. Результат округлите до сотых.

Решите уравнение: $$\sqrt<10-3x>=x-2$$

Если уравнение имеет более одного корня, в ответе укажите меньший из них.

$$-2\notin$$ ОДЗ $$\Rightarrow$$ 3 - корень

Четырёхугольник ABCD вписан в окружность, причём BC =CD. Известно, что угол ADC равен 93°. Найдите, под каким острым углом пересекаются диагонали этого четырёхугольника. Ответ дайте в градусах.

1) $$\bigtriangleup AOD\sim \bigtriangleup COB$$ $$\Rightarrow$$

$$\angle ADO=\angle OCB=\alpha$$

$$\angle DAO=\angle OBC=\beta$$

2) $$\bigtriangleup DOC\sim \bigtriangleup AOB$$ $$\Rightarrow$$

$$\bigtriangleup DCB$$ - равнобедренный

$$\angle COB=\angle DCB=\beta$$ $$\Rightarrow$$ $$\alpha+\beta=93^<\circ>$$

В правильной треугольной призме $$ABCA_<1>B_<1>C_<1>$$, стороны оснований которой равны 2, боковые ребра равны 1, проведите сечение через вершины $$ABC_<1>$$. Найдите его площадь.

2) Построим $$C_<1>H\perp AB$$, $$C_<1>H$$ - медиана, высота $$\Rightarrow$$

Найдите значение выражения: $$\frac\cdot\sqrt><\sqrt\cdot\sqrt>$$ при $$b=4$$

Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту с фиксированной начальной скоростью. Траектория полёта камня в системе координат, связанной с машиной, описывается формулой $$y=ax^<2>+bx$$, $$a=-\frac<1><25>$$, $$b=\frac<7><5>$$ постоянные параметры, x (м)-смещение камня по горизонтали, y (м)-высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 9 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?

Из городов A и B навстречу друг другу одновременно выехали с постоянными скоростями два автомобиля. Скорость первого автомобиля была в два раза больше скорости второго. Второй автомобиль прибыл в A на 1 час позже, чем первый прибыл в B. На сколько минут раньше произошла бы встреча автомобилей, если бы второй автомобиль ехал с той же скоростью, что и первый?

Пусть $$t_<1>$$ - время встречи в первом случае:

Пусть $$t_<2>$$ - во втором:

Найдите наименьшее значение функции $$y=\frac-6x+36>$$ на отрезке $$$$

а) Решите уравнение: $$7\sin(2x-\frac<5\pi><2>)+9\cos x+1=0$$

б) Укажите корни этого уравнения, принадлежащие отрезку $$[-\frac<3\pi><2>;\frac<\pi><3>]$$

Основание пирамиды DABC - прямоугольный треугольник ABC с прямым углом С. ВАысота пирамидыпроходит через середину ребра AC, а боковая грань ACD - равносторонний треугольник.

а) Докажите, что сечение пирамиды плоскостью, проходящей через ребро BC и произвольную точку M ребра AD, - прямоугольный треугольник.

б) Найдите расстояние от вершины D до этой плосктости, если M - середина ребра AD, а высота пирамиды ранва 6.

а) 1) Пусть $$DH$$ - высота; $$\Rightarrow DH\perp ABC$$

2) Пусть $$MC\cap DH=N\Rightarrow NH\perp AC$$

$$\Rightarrow CH$$ - проекция $$NC$$ на $$(ABC)$$

3) т.к. $$AC\perp CB$$, то по теореме о трех перпендикулярах $$NC\perp CB$$

$$\Rightarrow$$ $$MC\perp CB$$

$$\Rightarrow\bigtriangleup MCB$$ - прямоугольный

б) 1) т.к. $$AC\perp CB$$ и $$CB\perp MC$$ $$\Rightarrow CB\perp(ADC)$$

$$\Rightarrow$$ расстояние от D до $$(CBM)$$ - перпендикуляр $$DL\in(ADC)$$

2) т.к. $$\bigtriangleup ACD$$ - равносторонний и $$AM-MD, то $$CM\perp AD$$

$$\Rightarrow DM$$ - искомое расстояние

Выберем все кратные 3 из этого диапазона: $$12;15;18;21;24;27;30;33;36$$

$$2a+b=2$$ $$\Rightarrow$$ $$a=1;b=0$$ или $$a=0;b=2$$

$$2a+b=11$$ $$\Rightarrow$$ $$a=5;b=1$$ или $$a=4;b=3$$

Пенсионер гуляет по дорожкам парка каждой. Определение вероятности наступления события. Повторение испытаний. Формула Бернулли

Решение задачи

Задание 1. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 2. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Площадь треугольника АВС равна 28. DE – средняя линия. Найдите площадь трапеции ABDE.

Решение

Задание 3. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 4. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 5. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 6. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 7. Вариант 240 Ларина. ЕГЭ 2019 по математике.

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми ВА 1 и АС. Ответ дайте в градусах.

Решение

Задание 8. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите значение выражения при a=216

Задание 9. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 10. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 11. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите наименьшее значение функции y=4cosx+13x+9 на отрезке

Задание 12. Вариант 240 Ларина. ЕГЭ 2019 по математике.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку [-2пи;-пи/2]

Задание 13. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 14. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 15. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 16. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

Задание 17. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите все значения параметра a , при каждом из которых уравнение

имеет решения, и определите то решение, которое получается только при единственном значении параметра a .

Основы
теории
вероятностей
Чикрин Евгений
Александрович
КАЗАНЬ2016

вероятность
ОТВЕТ: 0,3

Примеры непосредственного определения вероятностей

ЗАДАЧА 4. Вероятность того, что чайник прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите

ЗАДАЧА 5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Веро

Основные правила вычисления вероятностей сложных событий

ЗАДАЧА 9. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Пенсионер н

Основные правила вычисления вероятностей сложных событий

Формула полной вероятности

Повторение испытаний. Формула Бернулли

ЗАДАЧА 14. За один выстрел стрелок поражает мишень с вероятностью 0,1. Найдите вероятность того, что при пяти выстрелах он хотя бы раз попадет

МБОУ Останкинская СШ

Подготовка к ЕГЭ

Решение задач по теории вероятности

В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

А – кофе закончится в первом автомате; В – кофе закончится во втором автомате.

По условию задачи,

отметим, что эти события не являются независимыми, в противном случае

Вероятность противоположного события «кофе останется в обоих автоматах» равна

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

4 варианта: ХХО, ХОО, ОХО, ООО

P(ХХО) + P(ХОО) + P(ОХО) + P(ООО)=0,8∙0,8∙0,2+0,8∙0,2∙0,8+

Яйцо куплено в 1 хозяйстве

Яйцо куплено во 2 хозяйстве

Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 30% всех телефонов этой марки,а вторая-остальные телефоны.Известно,что из всех телефонов,выпускаемых первой фабрикой,1% имеют скрытые дефекты,а у выпускаемых второй фабрикой-1,5%.Найдите вероятность того,что купленный в магазине телефон этой марки имеет скрытый дефект.

Д-телефон имеет дефект

Д-стекла имеют брак

Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G

Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S,другие –в поле F или в болото М.Найдите вероятность того, что Павел Иванович забредет в болото.

Событие A - в автобусе меньше 15 пассажиров

Событие В - в автобусе от 15 до 19 пассажиров

Событие A + B - в автобусе меньше 20 пассажиров

События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:

P(В) = 0,94 − 0,56 = 0,38.

P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B)

Событие A - учащийся решит 11 задач

Событие В - учащийся решит больше 11 задач

Событие A + B - учащийся решит больше 10 задач

Событие А –Джон возьмет

Событие В –Джон возьмет

не пристрелянный револьвер

Событие А-пациент болеет гепатитом

Событие В- пациент не болеет гепатитом

Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнет игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза

Перевести на монеты Так как 3 матча,то три раза бросается монета.

Событие А - орел выпадет 2 раза(в играх «Физик» выиграет жребий ровно два раза)

Пенсионер гуляет по дорожкам парка каждой. Определение вероятности наступления события. Повторение испытаний. Формула Бернулли

Решение задачи

Задание 1. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 2. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Площадь треугольника АВС равна 28. DE – средняя линия. Найдите площадь трапеции ABDE.

Решение

Задание 3. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 4. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 5. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 6. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 7. Вариант 240 Ларина. ЕГЭ 2019 по математике.

В кубе ABCDA 1 B 1 C 1 D 1 найдите угол между прямыми ВА 1 и АС. Ответ дайте в градусах.

Решение

Задание 8. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите значение выражения при a=216

Задание 9. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 10. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 11. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите наименьшее значение функции y=4cosx+13x+9 на отрезке

Задание 12. Вариант 240 Ларина. ЕГЭ 2019 по математике.

а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку [-2пи;-пи/2]

Задание 13. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 14. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Решение

Задание 15. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Задание 16. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.

Задание 17. Вариант 240 Ларина. ЕГЭ 2019 по математике.

Найдите все значения параметра a , при каждом из которых уравнение

имеет решения, и определите то решение, которое получается только при единственном значении параметра a .

Основы
теории
вероятностей
Чикрин Евгений
Александрович
КАЗАНЬ2016

вероятность
ОТВЕТ: 0,3

Примеры непосредственного определения вероятностей

ЗАДАЧА 4. Вероятность того, что чайник прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите

ЗАДАЧА 5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Веро

Основные правила вычисления вероятностей сложных событий

ЗАДАЧА 9. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Пенсионер н

Основные правила вычисления вероятностей сложных событий

Формула полной вероятности

Повторение испытаний. Формула Бернулли

ЗАДАЧА 14. За один выстрел стрелок поражает мишень с вероятностью 0,1. Найдите вероятность того, что при пяти выстрелах он хотя бы раз попадет

МБОУ Останкинская СШ

Подготовка к ЕГЭ

Решение задач по теории вероятности

А – кофе закончится в первом автомате; В – кофе закончится во втором автомате.

По условию задачи,

отметим, что эти события не являются независимыми, в противном случае

Вероятность противоположного события «кофе останется в обоих автоматах» равна

4 варианта: ХХО, ХОО, ОХО, ООО

P(ХХО) + P(ХОО) + P(ОХО) + P(ООО)=0,8∙0,8∙0,2+0,8∙0,2∙0,8+

Яйцо куплено в 1 хозяйстве

Яйцо куплено во 2 хозяйстве

Д-телефон имеет дефект

Д-стекла имеют брак

Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S,другие –в поле F или в болото М.Найдите вероятность того, что Павел Иванович забредет в болото.

Событие A - в автобусе меньше 15 пассажиров

Событие В - в автобусе от 15 до 19 пассажиров

Событие A + B - в автобусе меньше 20 пассажиров

События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий:

P(В) = 0,94 − 0,56 = 0,38.

P(A + B+ С) = P(A) + P(B)+ P(С)= P(A) + P(B)

Событие A - учащийся решит 11 задач

Событие В - учащийся решит больше 11 задач

Событие A + B - учащийся решит больше 10 задач

Событие А –Джон возьмет

Событие В –Джон возьмет

не пристрелянный револьвер

Событие А-пациент болеет гепатитом

Событие В- пациент не болеет гепатитом

Перевести на монеты Так как 3 матча,то три раза бросается монета.

Событие А - орел выпадет 2 раза(в играх «Физик» выиграет жребий ровно два раза)

ТЕСТ ЕГЭ - 2017 ПО МАТЕМАТИКЕ

ПРОФИЛЬНЫЙ УРОВЕНЬ

1. По тарифному плану "Просто как день" компания сотовой связи каждый вечер снимает со счета абонента 18 рублей. Если на счёте осталось меньше 18 рублей, то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 500 рублей. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?

2. При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси - напряжение в вольтах. Определите по рисунку, какое напряжение будет в цепи через 15 часов работы фонарика. Ответ дайте в вольтах.

3. Найдите площадь трапеции ABCD, изображённой на клетчатой бумаге с размером клетки 1 х 1 (см. рис.).

4. Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадёт в точку G.

5. Найдите корень уравнения

6. Четырёхугольник ABCD вписан в окружность. Угол АВС равен 132°, угол ABD равен 61°. Найдите угол CAD. Ответ дайте в градусах.

7. На рисунке изображены график функции у = f(x) и десять точек на оси абсцисс: х 1 , х 2 , х 3 , . х 10 . В скольких из этих точек производная f"(x) функции f(x) положительна?

8. Бетонный шар весит 0,5 т. Сколько тонн будет весить шар вдвое большего радиуса, сделанный из такого же бетона?

9. Найдите значение выражения

10. Коэффициент полезного действия некоторого двигателя определяется формулой

При каком значении температуры нагревателя Т 1 (в градусах Кельвина) КПД этого двигателя будет 80%, если температура холодильника Т 2 = 200 К?

11. Брюки дороже рубашки на 30% и дешевле пиджака на 22%. На сколько процентов рубашка дешевле пиждака?

у = 13х − 13tg x − 18

13. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку [−3; 1].

14. В правильной треугольной призме АВСА 1 В 1 С 1 сторона основания АВ = 7√3, а боковое ребро АА 1 = 8.

а) Докажите, что плоскость ВСА 1 перпендикулярна плоскости, проходящей через ребро АА 1 и середину ребра В 1 С 1 .

б) Найдите тангенс угла между плоскостями ВСА 1 и ВВ 1 С 1 .

15. Решите неравенство

16. На сторонах АС и ВС треугольника АВС вне треугольника построены квадраты ACDE и BFKC. Точка М - середина стороны АВ.

а) Докажите, что СМ = 1 / 2 · DK.

б) Найдите расстояние от точки М до центров квадратов, если АС = 14, ВС = 16 и угол АСВ = 150°.

17. В двух областях есть по 50 рабочих, каждый из которых готов трудиться по 10 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,2 кг алюминия или 0,1 кг никеля. Во второй области для добычи х кг алюминия в день требуется х 2 человеко-часов труда, а для добычи у кг никеля в день требуется у 2 человеко-часов труда.

Обе области поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 1 кг алюминия приходится 2 кг никеля. При этом области договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

«Колебание точки» - Промежуточная ситуация. Движение является затухающим и апериодичным. 5. Линейные колебания. 7. Свободные колебания с вязким сопротивлением. Общее решение = общее решение + частное решение однородного у-я неоднородного у-я. 1. Примеры колебаний. Гармоническая вынуждающая сила. Свободные колебания, вызванные вынуждающей силой.

«Производная функции в точке» - Какое значение принимает производная функции y=f(x) в точке В? На рисунке изображен график производной y= f‘(x) функции f(x) определенной на интервале (-3;3). Какое значение принимает производная функций y= f(x) в точке А? Какой угол образует касательная к графику функции с положительным направлением оси ох?

«Критические точки функции» - Среди критических точек есть точки экстремума. Необходимое условие экстремума. Критические точки функции Точки экстремумов. Определение. Точки экстремума (повторение). Но, если f" (х0) = 0, то необязательно, что точка х0 будет точкой экстремума. Примеры. Критические точки.

«Координаты точки» - Симметрия точки относительно оси абсцисс (Ох). Тело ящерицы симметрично относительно прямой. Тело человека имеет ось симметрии. В природе строение тел животных так же подчиняется законам симметрии. Точка В(3;6) симметрична точке В (3; - 6), расположенной ниже оси абсцисс. Вывод: Семиричник – редкое растение, но семь лепестков цветка имеют двустороннюю симметрию.

«ЮАР национальные парки» - «Путешествие в Южно-Африканскую республику». Поблизости расположен и знаменитый водопад Тугела (948 м.) из пяти каскадов. Третий день Национальные парки и заповедники. Первый день Столица ЮАР. Стоимость номеров в отеле начинается от $400. В облаке водяной пыли, поднимающемся на 100 метров, светится радуга.

«Четыре замечательные точки треугольника» - Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называется. Высота. Медианой треугольника. Задача № 1. Высотой треугольника. Отрезок АН – перпендикуляр, опущенный из точки А на прямую а, если. Отрезок, соединяющий вершину с серединой противолежащей стороны, называется.

Просмотр содержимого документа
«Как решать задачи на вероятность»

Митрофанова Снежана Викторовна, МБОУ «Верховская школа» Вологодская область

Тема: Практикум по решению задач по теории вероятности.

Как решать задачи на вероятность?

Вероятность. Что это?

Теория вероятностей , как следует из названия, имеет дело с вероятностями. Нас окружают множество вещей и явлений, о которых, как бы ни была развита наука, нельзя сделать точных прогнозов. Мы не знаем, какую карту вытянем из колоды наугад или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, можем строить прогнозы и вычислять вероятности этих случайных событий.

Таким образом, мы сталкиваемся с основным понятием случайного события -это явления, поведение которого невозможно предсказать, или это опыта, результат которого заранее невозможно вычислить и т.п. Именно вероятности событий вычисляются в типовых задачах ЕГЭ.

СЛАЙД 2 (ЕЩЁ РАЗ)

Вероятность - это некоторая, строго говоря, функция, принимающая значения от 0 до 1 и характеризующая данное случайное событие.

Затем используем примерную схему , по которой следует решать стандартные учебные задачи на вычисление вероятности случайного события,

а затем ниже на примерах я проиллюстрирую ее применение.

Найти основной вопрос задачи(найти что является исход задачи, найти благоприятные исходы.)

Выбрать формулу (или несколько) для решения.

ПОЧЕМУ МЫ ВНИМАТЕЛЬНО ЧИТАЕМ ЗАДАЧИ?

Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник сможет ответить на выбранный наугад билет?

Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник не сможет ответить на выбранный наугад билет?

0,5 · 0,25= 0,125

СЛАЙД 19, 20

Просмотр содержимого презентации
«Презентация»

Как решать задачи

на вероятность?

Митрофанова Снежана Викторовна,

МБОУ «Верховская школа»

Вероятность.Что это ?

Вероятность - это некоторая функция, принимающая значения от 0 до 1.

Примерная схема , по которой следует решать стандартные учебные задачи на вычисление вероятности:

Найти основной вопрос задачи

Выбрана формула (или несколько) для решения.

Вероятностью события называется отношение числа исходов, благоприятствующих его наступлению к числу всех исходов (несовместных, единственно возможных и равновозможных):

Задачи, решаемые с помощью построения дерева вероятностей.

Задача 1. Павел Иванович совершает прогулку из точки A по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку G .

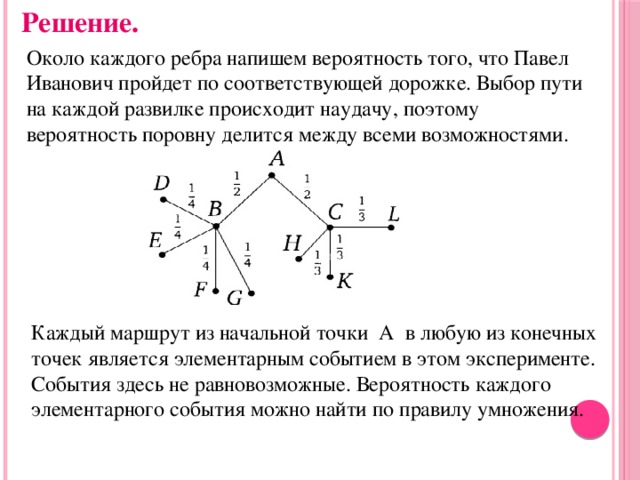
Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями.

Каждый маршрут из начальной точки A в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.

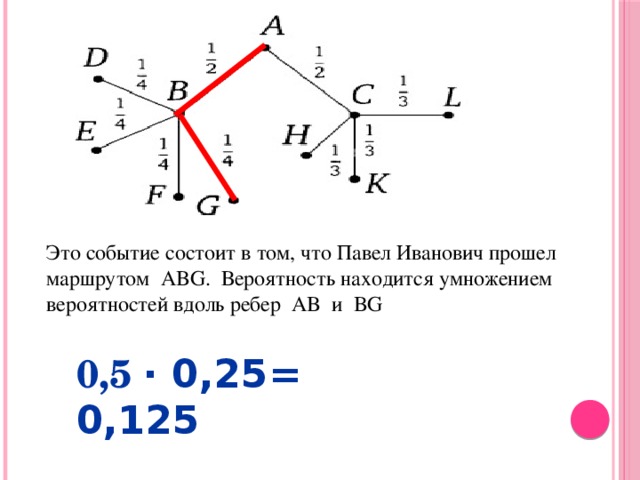
Это событие состоит в том, что Павел Иванович прошел маршрутом ABG. Вероятность находится умножением вероятностей вдоль ребер AB и BG

0,5 · 0,25= 0,125

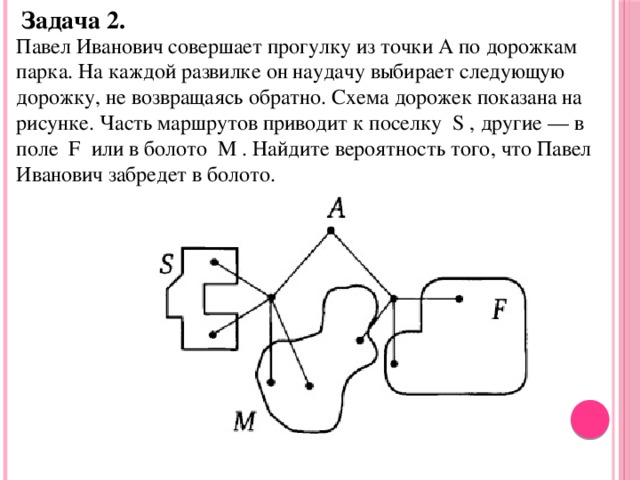
Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S , другие - в поле F или в болото M . Найдите вероятность того, что Павел Иванович забредет в болото.

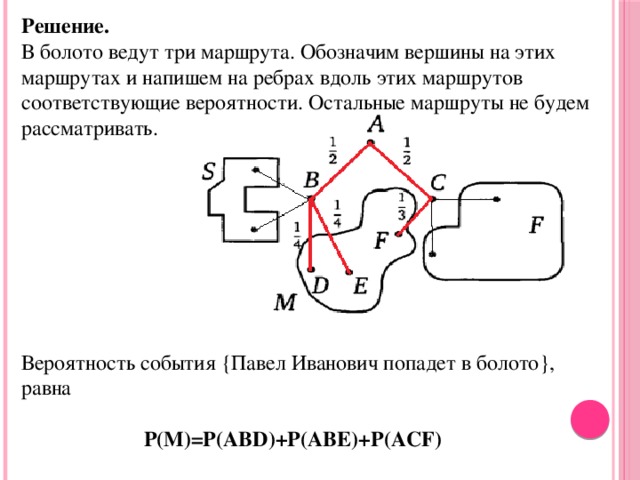
Решение. В болото ведут три маршрута. Обозначим вершины на этих маршрутах и напишем на ребрах вдоль этих маршрутов соответствующие вероятности. Остальные маршруты не будем рассматривать.

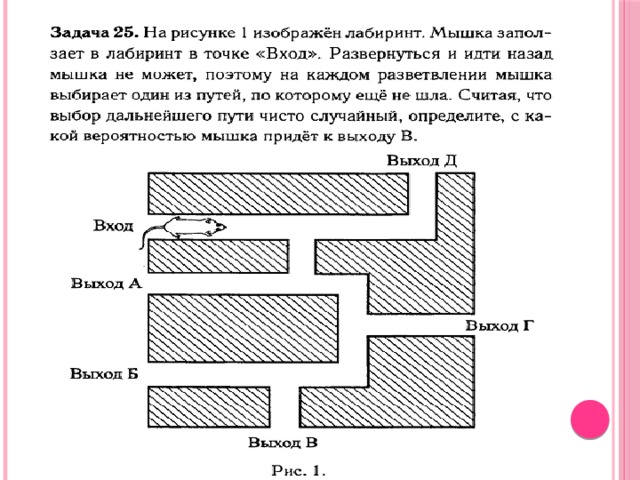
Ответ: 0,125

Задача 4. Две фабрики одной фирмы выпускают одинаковые мобильные телефоны.

Первая фабрика выпускает 30 % всех телефонов этой марки, а вторая - остальные телефоны.

Известно, что из всех телефонов, выпускаемых первой фабрикой, 1 % имеют скрытые дефекты, а у выпускаемых второй фабрикой - 1,5 %.

Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.

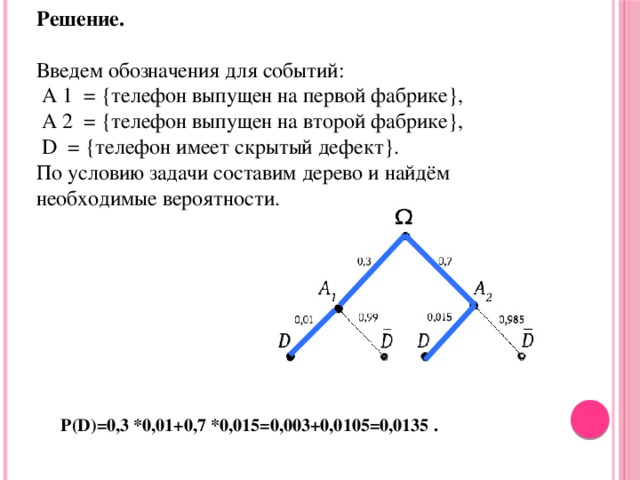
Решение. Введем обозначения для событий: A 1 = <телефон выпущен на первой фабрике>, A 2 = <телефон выпущен на второй фабрике>, D = <телефон имеет скрытый дефект>. По условию задачи составим дерево и найдём необходимые вероятности.

P(D)=0,3 *0,01+0,7 *0,015=0,003+0,0105=0,0135 .

Решение задачи

Читайте также: