Два гениальных математика не достигшие пенсионного возраста встретились после долгого перерыва

Игра Эврика! логические задачи - ответы и подсказки к приложению для телефона и планшета (android), iphone и ipad (ios). Решения и пояснения на все уровни игры.

Игра "Эврика" ответы: УРОВЕНЬ 51

Вопрос: Дворник Петя проходил со своей сестрой мимо дома номер 5. Он сказал, что зайдет навестить своего племянника. Сестра сказала: «Хорошо, поскольку у меня нет племянника, я пойду к себе домой». Кем приходится сестра загадочному племяннику?

Ответ: МАТЬ.

Решение: Сестра была матерью мальчика.

Игра "Эврика" ответы: УРОВЕНЬ 52

Вопрос: Приятельницы пили чай с молоком. Отпив половину чашки чая, Маша долила в чашку молока доверху. Затем Маша отпила третью часть получившегося чая с молоком и долила столько же молока. Затем она отпила шестую часть получившегося чая с молоком, дополнила чашку молоком доверху и выпила все до конца. Чего в итоге Маша выпила больше: молока или чая?

Ответ: ОДИНАКОВО.

Решение: Чая Маша выпила ровно один стакан, потому что изначально была 1 чашка чая и его не доливали. Соответственно, молока затем долили половину стакана, а это 1/2 его часть, затем опять долили молоко, на этот раз уже 1/3 стакана, а последний раз молока добавили уже 1/6 чашки. Получается, что сумма этих частей дает 1/2 + 1/3 + 1/6 = 1 стакан.

Игра "Эврика" ответы: УРОВЕНЬ 53

Вопрос: Если один кубический метр разделить на составляющие его кубические миллиметры и соединить их между собой гранями в одну прямую линию, то какой длины окажется эта линия? Дайте ответ в метрах.

Ответ: 1000000.

Решение: В одном кубическом метре 1000 x 1000 x 1000 кубических миллиметров.
В кубе, в 1 кубическом миллиметре, грань имеет длину также один миллиметр. Получается, что линия будет равняться длине 1 000 * 1 000 * 1 000 * 1 = 1 000 000 000 миллиметров. Значит в метрах это 1 000 000. А в километрах будет 1000.

Игра "Эврика" ответы: УРОВЕНЬ 54

Вопрос: Вам дали это, это и сейчас принадлежит вам. Вы его никогда никому не передавали, но им пользуются все ваши знакомые. Что это?

Игра "Эврика" ответы: УРОВЕНЬ 55

Вопрос: Четыре супружеские пары отмечали день рождения. За чаепитием Лена съела 3 конфеты, Катя – 2 конфеты, Алина – 4, и Аня – одну конфету. Антон съел столько же, сколько и его жена, Илья – вдвое больше своей жены, Александр – в три раза больше своей жены, и Алексей – в 4 раза больше своей жены. Если все присутствующие съели вместе 32 конфеты, то не могли бы вы сказать, как зовут жену Александра?

Решение: Александр женат на Ане, съел 3 конфеты. Антон женат на Лене, съел 3 конфеты. Илья - на Алине, съел 8 конфет. Алексей - на Кате, съел 8 конфет.

Игра "Эврика" ответы: УРОВЕНЬ 56

Вопрос: В мешке лежит 101 монета. Среди них есть одна фальшивая, которая отличается от других по весу. Находить фальшивую монету не требуется. За какое количество взвешиваний можно определить легче или тяжелее фальшивая монета?

Решение: Сначала необходимо взвесить 50 и 50 монет. Если они будут равны по весу, то нужно взять оставшуюся одну монету и поставить ее в левую кучку (или в правую, тут неважно в какую кучку, ведь в той и другой изначально по 50 монет) вместо одной из имеющихся там. Далее смотрим, если левая кучка тяжелее, следовательно, фальшивая монета тяжелее. Если левая кучка легче, следовательно, фальшивая монета легче.
Если же кучки по 50 и 50 монет не равны, то берем более тяжелую кучку и разбиваем ее на две кучки по 25 монет. Если вес кучек одинаковый, следовательно, фальшивая монета легче. Если вес кучек неодинаковый, следовательно, фальшивая монета тяжелее, чем настоящие монеты.

Игра "Эврика" ответы: УРОВЕНЬ 57

Вопрос: Группа школьников отправилась в велопоход. Первоклассники ехали на трехколесных, а старшеклассники – на двухколесных велосипедах. Сколько старшеклассников отправилось в поход , если известно, что общее количество колес равно 12?

Решение: В задаче указано множественное число участников велопохода (первоклассники и старшеклассники), значит их 2 и больше. Предположим, что всего 2 первоклассника на трехколесном велосипеде, значит общее количество их колес 6, остается еще 6 колес.
Так как старшеклассников тоже либо 2, либо больше. Значит минимальное количество их колес это 4. Соответственно, 6+4 = 10, остается еще 2 колеса, значит с ними ехал еще один старшеклассник на двухколесном велосипеде.
Итак, три старшеклассника ехали на двухколесном велосипеде и 2 первоклассника ехали на трехколесном велосипеде.

Игра "Эврика" ответы: УРОВЕНЬ 58

Вопрос: Группа пенсионеров играла во дворе в лото. В разгар азарта одна фишка отлетела и разбила фару запорожца дворника Петровича. Захарыч сказал: «Это или Никитич, или Львович». Никитич сказал: «Это сделал не я и не Платоныч». Иваныч сказал: «По-моему, один из них говорит правду, а другой – нет». А Платоныч сказал: Иваныч, ты ошибаешься». А жена дворника в тот момент сидела на лавочке и все видела. Она сказала, что только один пенсионер солгал, но, из-под чьей же руки вылетела роковая фишка, не рассказала. Но ведь вы и сами догадаетесь.

Ответ: ЛЬВОВИЧ.

Решение: Про разбитую фару обманул только Иваныч. Так как Захарыч сказал правду о том, что это или Никитич, или Львович. А Никитич сказал правду про себя, что он не разбивал фару, и Платоныч не разбивал.

Игра "Эврика" ответы: УРОВЕНЬ 59

Вопрос: Старые друзья собрались в баре и стали обсуждать подарки, которые каждый из них преподнес своей жене на 8 марта. Один заявил, что его подарок может разогнаться до 100 км/ч за 6 секунд, это "Порше". Второй сказал, что подарил жене "Феррари" - до 100 за 4 секунды. А третий сообщил, что его подарок достигает 100 за 2 секунды, что совершенно не радует его жену. Что подарил третий мужчина?

Ответ: ВЕСЫ.

Игра "Эврика" ответы: УРОВЕНЬ 60

Вопрос: В какой-то момент он остановился около одного предмета и сказал: "Это красная". Мама возразила: "Нет, она черная." "Почему же она белая?" - спросил Вова. "А потому, что зеленая." Что обсуждал Вова с мамой?

Ответ: СМОРОДИНА.

Игра "Эврика" ответы: УРОВЕНЬ 61

Вопрос: Вася выписал на доске все пятизначные числа, у которых каждая цифра либо равна обеим соседним, либо отличается от соседних ровно на единицу - от одного в меньшую, а от другого в большую сторону. Сколько написанных Васей чисел имеют в своей записи цифру "5"?

Решение: 12345 23456 34567 45678 56789 - это пять чисел
обратные: 98765 87654 76543 65432 54321 - это ещё пять чисел
и плюс одно 55555 - итого одиннадцать.

Игра "Эврика" ответы: УРОВЕНЬ 62

Вопрос: Два гениальных математика, не достигшие пенсионного возраста, встретились после долгого перерыва, чтобы прогуляться по аллее. Петя в это время сидел в кустах и подслушал их странный разговор:
- Ну а дети у тебя есть?
- Три сына.
- А сколько им лет?
- Если перемножить, будет как раз твой возраст.
- (Немного подумав). Мне этих данных не достаточно.
- Еще если сложить их возраст, получится сегодняшнее число.
- (Вновь после размышления). Нет. пока не могу вычислить.
- Ну так средний сын любит танцевать.
- А, теперь ясно!
Петя в кустах впал в ступор. А Вы сможете определить возраст каждого из сыновей (запишите возрасты цифрами через пробел без запятых)?

Ответ: 1 5 8.

Решение: Математик знает произведение и сумму трех целых числе и не может их определить. Значит, эти числа такие, что их нельзя однозначно определить, таким образом сумма и произведение двух троек чисел равны. Дальше, путем перебора всех возможных чисел, которые могут быть по условию задачи, например, можно перебрать от 20 до 60 лет, тогда можно понять, что почти во всех этих случаях эти числа раскладываются на произведение из трех сомножителей, которые имеют разные суммы. Получается, что есть только 2 исключения:
36 = 1 * 6 * 6 = 2 * 2 * 9, тогда суммы множителей равны 13,
40 = 2 * 2 * 10 = 1 * 5 * 8, тут суммы множителей равны 14.
Соответственно, подходит лишь последний вариант, в так как последняя подсказка исключает детей одинакового возраст.

Игра "Эврика" ответы: УРОВЕНЬ 63

Вопрос: Маленький гномик оформлял книгу детских сказок. Он уже закончил с рисунками и приступил к проставлению номеров страниц. Для этого ему потребовалось 534 цифры. Он ставил номер на каждой странице, начиная с первой. Сколько же страниц в учебнике?

Решение: Для нумерации с 10 страницы по 99 страницу использовано уже 2 цифры, получается, что 180 цифр ((99 - 10) * 2 цифры в каждом числе + 2 цифры в числе 10). Для нумерации с 100 страницы по 200 страницу будет использовано 303 цифры ((200 - 100) * 3 цифры в каждом числе + 3 цифры в числе 100).
Итого использовано 492 цифры (9 + 180 + 303).
534 цифры потребовались маленькому гномику – 492 цифры, полученные с цифры в итоге = 42 цифр остается. 42 цифры делим на 3 (так как следующее число будет трехзначным, а именно 201) и получаем 14, соответственно, 200 + 14 = 214 страниц было пронумеровано гномиком.

Игра "Эврика" ответы: УРОВЕНЬ 64

Вопрос: Винни-Пух и Пяточек нашли два одинаковых кирпича. Они положили их на гладкую доску: один плашмя, а другой – на ребро. Им очень хотелось узнать, какой кирпич соскользнет первым, если начать наклонять доску.

Ответ: ОБА или ОДИНАКОВО.

Решение: Кирпичи начнут скользит одновременно, оба одновременно. Ведь сразу оба кирпича давят на гладкую доску с одинаковой силой. А это значит, одинаковы и силы трения, которые приходится им преодолевать при скольжении по гладкой доске. Удельные силы трения, приходящиеся на каждый квадратный сантиметр площади соприкосновения кирпичей с доской, разумеется, не равны. Но общие силы трения, действующие на кирпичи, которые равны произведению удельной силы трения на площадь поверхности соприкосновения, получается одинаковые.

Игра "Эврика" ответы: УРОВЕНЬ 65

Вопрос: Белка и Стрелка летели на вертолете из Байконура. Поднявшись в воздух, вертолет пролетел строго на север 500 км, потом повернул на восток и пролетел еще 500 км, далее повернул на юг и пролетел еще 500 км, и, наконец, повернув на запад, пролетел последние 500 км. Где он приземлился (введите номер варианта ответа)?
1) там же, откуда вылетел
2) севернее
3) южнее
4) западнее
5) восточнее

Решение: Восточнее места вылета. Меридианы Земли сближаются к северу, а вертолет летел не по квадрату, а по трапеции.

Игра "Эврика" ответы: УРОВЕНЬ 66

Вопрос: Четыре приятеля решили подарить девушкам цветы. Утром следующего дня никто не смог точно вспомнить, что было вчера до общей попойки и кто кому подарил какие цветы. Совместными усилиями удалось вспомнить, что:
1. Каждой из четырех девушек подарили один букет;
2. У всех девушек были разные цветы;
3. Юрий целый день не видел Катю и Марину;
4. Дима не смог купить букет роз;
5. Андрей не дарил цветов ни Оле, ни Марине;
6. Георгий сначала хотел подарить букет Лене или Кате, но потом передумал;
7. Ни Лена, ни Оля не встречались с Димой;
8. Катя так и не получила свои любимые мимозы;
9. Андрей не покупал цветов на букву "Г";
10. Ни Лене, ни Оле не дарили роз;
11. Юрий не успел купить гладиолусы;
12. Георгий помнил, что видел у своих друзей букеты гвоздик и мимоз;
13. В итоге у Марины не оказалось гвоздик и гладиолусов, которые она ожидала получить;
14. Лена хвасталась подруге, что ей "не подарили этих дешевых мимоз".
Кто и что подарил Кате?

Ответ: АНДРЕЙ РОЗЫ.

Решение: Юрий подарил гвоздики Лене. Андрей подарил розы Кате. Дима подарил мимозы Марине. Георгий подарил гладиолусы Оле.

Игра "Эврика" ответы: УРОВЕНЬ 67

Вопрос: В рассказе А. П. Чехова "Репетитор" гимназист Егор Зиберов не сумел решить арифметическую задачу, а отец репетируемого ученика, отставной губернский секретарь Удодов, пощелкав на счетах, получил правильный ответ. Решите и Вы эту задачу арифметически? Вот она.
Купец купил 138 аршин черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он и того другого, если синее стоило 5 руб за аршин, а черное - 3 руб.?

Ответ: 75 63.

Решение: Если бы купец приобрел сукно одного типа, например, синее, тогда он заплатит за него 138 * 5 рублей получается 690 рублей. Образовавшаяся разность в 150 рублей получена за счет того, что черное сукно повышено в цене ровно на 2 рубля. Получается, что черного сукна было 150 / 2 = 75 аршин, а синего сукна получается 138 – 75 = 63 аршина.

Два математика, не достигшие пенсионного возраста, встретились после долгого перерыва. Приведем фрагмент их диалога:
- Ну, а дети у тебя есть?
- Три сына.
- А сколько им лет?
- Если перемножить, будет как раз твой возраст.
- (После размышления.) Мне этих данных недостаточно.
- Если сложить их возраст, получится сегодняшнее число.
- (Вновь после размышления.). Все еще не понимаю.
- Кстати, средний сын любит танцевать.
- Понял.
А Вы можете определить возраст каждого из сыновей?

Ответ: Математик знает произведение и сумму трех целых чисел и не может их определить. Значит, эти числа таковы, что их нельзя однозначно определить. Если переберем все натуральные числа в разумных пределах, соответствующих условию задачи, например, от 20 до 60, то убедимся, что почти во всех случаях эти числа раскладываются на произведение из трех сомножителей, имеющих разные суммы. Есть только два исключения:

36 = 1*6*6 = 2*2*9, суммы множителей равны 13,

40 = 2*2*10 = 1*5*8, суммы множителей равны 14.

Подходит лишь последний вариант, в котором есть средний сын. Итак, возраст 1 год, 5 и 8 лет.

"Если переберем все натуральные числа в разумных пределах, соответствующих условию задачи, например, от 20 до 60, то убедимся, что почти во всех случаях эти числа раскладываются на произведение из трех сомножителей, имеющих разные суммы. Есть только два исключения. "

Оставлен Гость Ср, 08/25/2010 - 16:37

"почти во всех случаях эти числа раскладываются на произведение из трех сомножителей, имеющих разные суммы. Есть только два исключения"

а почему эти суммы должны быть одинаковые.

Оставлен Гость Ср, 10/27/2010 - 14:16

Потому что второй математик задал уточняющий вопрос, и ему намекнули, что дети разновозрастные! Были сомнения значит у вопрошающего математика, были варианты, а термин "средний" избавил его от этих сомнений.

Оставлен Гость Ср, 11/17/2010 - 08:11

Дошло наконец! :-)
Если отбросить то, что детям может быть полтора года, 2 с половиной года и т.д., а взять только целую часть (1, 2, и т.д.), получаем (в порядке "получения информации"):

1) ЦЕЛОЕ ЧИСЛО (возраст, чтоб наверняка, возьмём от 20 до 65), его можно (МОЖНО почти всегда) разложить на РАЗНЫЕ 3 сомножителя (поэтому 1-й ответ "Мне этих данных недостаточно." Ведь даже зная число (свой возраст) ответом могут быть разные комбинации сомножителей и однозначно дать ответ нельзя).

2) ЦЕЛОЕ ЧИСЛО (дата), но т.к. РАЗНЫЕ сомножители дают (почти всегда) РАЗНЫЕ суммы (даты), то математик сразу бы дал ответ. Но и этих данных ему недостаточно.

===> Значит дата дня их разговора (число от 1 до 31) может по-разному раскладываться на суммируемые элементы, которые перемножатся в одно и то же число.
среди чисел от 1 до 31 есть 2 таких числа:
"36 = 1*6*6 = 2*2*9, суммы множителей равны 13,
40 = 2*2*10 = 1*5*8, суммы множителей равны 14."
(поэтому 2-й ответ "Все еще не понимаю." Т.к. у математика 2 варианта - на конкретный свой возраст-произведение и конкретную дату-сумму)

3) ТОГДА МЫ УЗНАЁМ, ЧТО ЕСТЬ СРЕДНИЙ СЫН ===> все три возраста разные,
а это единственный вариант 1*5*8.
Надеюсь тем, кому, как и мне, не сразу дошло, тоже дошло. :-)

Оставлен обычный человек! Ср, 11/24/2010 - 06:43

Ответов может быть несколько, так как в задачи нет возраста второго математика и нет конкретной даты, исходя из этого
невозможно определить точные возроста детей. 1*5*8 - бред не сказано же, что 2 математику 40 лет и 14 число в которое они болтали,) нет таких данных.
так что можно привести любые комбинации, но чтобы устраивал условия задачи!)) например: 1*6*9 - полностью устраивает условию задачи, 2 математику 54 года и 16 число))

Оставлен Лев Вс, 01/30/2011 - 23:50

нет, правильный ответ 1, 5, 8. объясняю:
если рассмотреть ваш вариант, то что мы видим
1) на первые вопрос о возрасте, второй математик получил ответ: их произведение 54
он математик, и быстро подсчитал, что есть несколько вариантов возрастов - 1, 6, 9; 1, 2, 27 (может первый математик развёлся с первой женой, и женился снова 3 года назад) 1, 3, 18 и так далее. точного ответа, какой возраст у детей он дать не может, и просит подсказку
2) их сумма равна нынешней дате (16)
он перебирает варианты из 1, в поисках подходящего
1+6+9=16, 1+2+27=30, 1+3+18=24 и т.д. он знает дату, и (в данном случае) получает один вариант: 1, 6, 9, но по условию самой задаче, ему нехватило данных, и он попросил ещё одну подсказку (то что у детей разные возраста). а в данном примере данных достаточно, и мы сразу получаем ответ

кстати, обратите внимание, что нам (людям. решающим задачу) приходится тяжелее, чем математику из неё, поскольку в отличии от него мы не знаем ни возраст, ни дату, а должны вычислить и их

Оставлен Гость Сб, 02/12/2011 - 07:04

бред какой-то почему 2, 5,6 не подходит
в 5 лет можно танцевать
2*5*6=60 вполне удовлетворяющий возраст, сумма 13

Оставлен Гость Сб, 04/09/2011 - 19:26

максимально возможное число 45
x=1
y=5
z=9

Оставлен HENRI Чт, 04/14/2011 - 15:25

2.4.5 TOJE PODXODIT

Оставлен Алекс Чт, 10/13/2016 - 20:48

Надо объяснять правильно Гость! Я даже не решал, но думаю что это поможет тем, кто не может понять)
1) мужик знает свой возраст! Но ответ не может дать, потому что есть минимум 2 совпадения. Нам труднее, и поэтому мы выбираем все варианты с минимум 2мя совпадениями!
2) математику дали 2 подсказку. Он знает дату. Теперь из тех вариантов, что выбрали после первого вопроса, он не смог выбрать, потому что опять осталось минимум 2 варианта! Нам опять тяжелее. В месяце максимально 31 день. Поэтому мы выбираем те варианты, которые меньше 31 и их несколько!
3) и последняя подсказка, что возрасты детей разные! И тады остается 1 ответ.

Оставлен Одьга Сб, 04/07/2018 - 16:08

А ничего, что 40 равно еще и 4*5*2, сумма множителей не равна 14

Оставлен Гость Пт, 01/25/2019 - 12:57

А почему ответом не может быть 1, 5.7? Тоже подходит.

Оставлен Гость Сб, 02/21/2015 - 10:41

1 7 8 разве не подходит. 1 6 8. 1 5 9.

Оставлен Алекс Чт, 10/13/2016 - 20:54

Математик знает свой возраст. У вас разные ответы 48 лет и 45 лет) должно совпадать

Оставлен Гость Ср, 07/07/2010 - 06:37

здесь нету ответа. пенсионный возраст 60лет, а им не сказано сколько так что может и 59 и 58 и т.д и во сколько лет они сделали детей тоже не сказано это может 19 или 21. так что это не реально вычислить. может это вообще тройня и всем одинаково.

Оставлен Гость Ср, 03/16/2011 - 18:02

Не может быть тройня. Там сказано, что был средний сын.

Оставлен Гость Чт, 07/08/2010 - 08:53

Оставлен Гость Ср, 07/14/2010 - 15:44

пенсионный возраст не имеет значения, так как по условию задичи "- Если сложить их возраст, получится сегодняшнее число." а число не может более 31! так как в месяце максимум 31 день

Оставлен admin Ср, 07/14/2010 - 23:56

Складывают возраст детей, а не отцов. А предпенсионный возраст нужен в предыдущем условии - при перемножении возрастов детей

Оставлен Гость Пт, 08/06/2010 - 17:40

а при чем тут тогда танцы? ведь второй понял все только после этой фразы =\\\

Оставлен Гость Чт, 09/09/2010 - 13:32

в этом предложение главное слово не "танцы", а "средний", т.е. значит нет близнецов и возраст у всех разный

Оставлен Елена Пнд, 10/25/2010 - 12:39

А почему только средний любит танцевать? дети могут и любят танцевать хоть в год, хоть в 10..

Оставлен Слава Сб, 08/07/2010 - 01:41

Разбираем условие по порядку
1)есть Математик(М) не достигший пенсионного возраста=> его возраст не менее 40 и не более 60. (думаю это ясно)
2)три сына(а,в,с)
авс=М;а+в+с=дата=>а+в+с 3)средний сын любит танцы. используя дедуктивный метод мышления можно прийти к выводу что если сын средний, то есть старший и младший. это раз! раз сын любит танцы, значит умеет ходить. в танцевальную секцию детей берут приблизительно в 5 лет..
Выводы: а5,c Решение:берем число 40(минимальный возраст М) и сразу раскладываем его на множители..40=1*5*8; 1+5+8=14. Все условия соблюдены.
Ответ:а=1;в=5;с=8 М=40;дата=14

Оставлен Слава Сб, 08/07/2010 - 01:51

Выводы: а извиняюсь за недочеты.. в5 это случайность. и возраста отца по условию нет. но на основе логики делаем такое смелое предположение что сын точно не старше 40 так как большая вероятность того что отец тогда достиг пенсионного возраста.

Оставлен Гость Ср, 10/13/2010 - 18:02

Не понимаю. А чем ответ 2, 4 и 8 лет не подходит? Не корректная задача!

Оставлен Гость Ср, 10/13/2010 - 18:04

. то есть 2, 4 и 6 (сори)

Оставлен Гость Сб, 02/19/2011 - 18:41

"есть Математик(М) не достигший пенсионного возраста=> его возраст не менее 40 и не более 60. " - утверждение не логично, так как нижняя планка возраста, думаю, может быть и 22 года (закончил университет но ещё не достиг пенсионного возраста).

Оставлен Avlek Пт, 09/03/2010 - 09:59

а что? Отец не может знать, кто из близнецов старше, а следовательно кто является средним сыном? условие задачи некорректное, я получил два ответа 1,6,6 и 1,5,8; я исходил из случая, что "2х летний не умеет танцевать" если все же умеет и любит, то получим четыре ответа

Оставлен Гость Пт, 10/01/2010 - 11:43

Мда. Вы посмотрите на ответы второго математика. Старость не радость.

Оставлен МС Сб, 11/06/2010 - 20:19

мда. совершенно некорректная задача. куча решений, если принять возраст первого ребенка в 1 год. и даже если в 2 - то одно подходит: 2, 3 и 4 года.

Оставлен МС Сб, 11/06/2010 - 20:24

даже не одно. и с первым ребенком в 2 года - тоже много решений.

Оставлен Гость Втр, 11/16/2010 - 13:58

вы идиоты все что-ли? до того как он узнал о среднем сыне, он не мог вычислить ответ, зная дату, тоесть было 2 или более вариантов перемножений 3 чисел, поэтому и пишут в ответе что есть только 2 числа с 2 вариантами 3 множителей, но одно из них имеет по 2 одинаковых числа в каждом варианте,а другое нет. 1 5 и 8

Оставлен Гость Вс, 11/21/2010 - 10:16

А если вариант такой:"2,4,5" ?
Произведение равно 40,это вписывается в рамки возраста от 40 до 65.
Сумма равна 11.Такая дата есть.
Есть средний сын,возраст которого 4 года,в этом возрасте некоторые дети прекрасно танцуют.

Оставлен Катя Втр, 11/30/2010 - 12:18

задача мне очень нравится я люблю решать такое!Катя 7 лет

Оставлен Гость Пт, 12/03/2010 - 07:08

Я бы рассмотрел числа от 60 вниз:59-простое число,не подходит;58-при делении пополам тоже получается простое число 29,не подходит,т.к. должно делиться;57-не подходит по предыдущей причине;56-раскладывается на 2*2*2*7.Искомое сочетание 2,4,7.Сумма 13.Чем не вариант?

Оставлен Гость Пнд, 01/31/2011 - 20:48

Тупорылая задача так как есть варианты от 1 до 31 и не однонго не известного мы можем единственное написать формулу под эту задачу.

Оставлен Миша 3 года Вс, 02/13/2011 - 16:12

Мне тоже очень нравится.Миша 3 года.

Оставлен Огненная Нежность Чт, 03/17/2011 - 00:20

Блин!Тут море вариантов. И каждый вполне удовлетворит условия.

1.Возраст ДО пенсионный?То есть до 65?Тогда смотрим от 18 до 65.

2.Перемножить возраст сыновей и выйдет возраст математика?

Я перебрала ВСЕ варианты..Вот к примеру такой. 9,3,2. Перемножить. 54 года.Подходит по условию?

3.Сумма даст сегодняшнее число?Значит до 31го..так? Складываем. 9+3+2. 14 Есть такой день в месяце.

4.Средний любит танцевать?Хорошо.Есть средний и ему 3 года..Почему бы в три годика не любить танцевать.

А вот если бы профессор сказал,что средний любит ЧИТАТЬ..то тут мой бы вариант не подходил..Только если сын гений))))

Оставлен Слава Вс, 04/17/2011 - 18:06

правильно детка,только забыла указать что возможны к примеру варианты не 9,3,2 а могло быть 18,3,1-
это первое условие:(вариативность,поэтому математик задал второй вопрос.)

Оставлен Гость Ср, 11/02/2011 - 07:01

Допенсионный возраст это до 60, 60-уже пенсионный возраст!

Оставлен Гость Ср, 03/30/2011 - 18:56

почему некоторым тугодумам так сложно прочесть разъяснения более умных товарищей? "бред какой-то почему 2, 5,6 не подходит в 5 лет можно танцевать "- кто тебе говорит, что в 5 нельзя танцевать? просто если взять 2, 5 и 6 , то диалог математиков получается бессмысленным:
- А сколько им лет?
- Если перемножить, будет как раз твой возраст.("2*5*6=60". из данного варианта следует, что он делит 60 на множители: 2, 2, 3, 5. Ему не достаточно данных, так как возможны несколько вариантов: 2,5,6; 3,4,5,; 2,2,15;2,3,10).
-Если сложить их возраст, получится сегодняшнее число.("2+5+6=13". но из возможных вариантов только 2, 5,6 дают 13. поэтому математик тут же и додумался бы , что именно 2,5,6 подходят. но из диалога следует , что данных ему все еще не достаточно."Все еще не понимаю". чтобы угадать возраст сыновей ему надо было узнать, что есть средний сын , т.е. возраст у сыновей разный. почему? потому что в его случае было два варианта набора чисел, которые давали дату и его возраст . а это возможно только в варианте с 1,5,8. т.е. ему было 40. он делит 40 на множители: 2, 2, 2,5. вариантов куча. идем дальше. сумма равна 14. Все еще два варианта: 2,2,10 и 1,5,8. тут собеседник говорит "Кстати, средний сын любит танцевать"- отсюда следует, что возраст у всех трех сыновей разный. остается 1 вариант: 1,5,8.

Оставлен Сергей Ср, 04/06/2011 - 17:55

В отличие от нас,второй "математик"знал и свой возраст и число месяца. После первого вопроса были два варианта ответа-1 ,5, 8 и 2, 4, 5.После второго вопроса вариантов не стало. К чему был третий вопрос? По-моему у этого "математика" фальшивый диплом!

Оставлен Гость Сб, 04/23/2011 - 21:59

мда, сколько тугодумов))

Оставлен Гость Ср, 04/27/2011 - 11:29

а если усложнить задачу:
суммарный возраст детей - 36. если перемножить возрасты детей, то тоже получится 36. один из детей старше остальных. сколько каждому лет? (ответа я сам не знаю)

Оставлен Гость Ср, 05/25/2011 - 12:36

Ответ логичен, но задача - нет. Искать решение тупым перебором - это не задача на логику. Pivot table заменит мозг.

Оставлен Гость Ср, 01/25/2012 - 08:22

Математику явно легче, он знает свой возраст и сегодняшнее число :)

Оставлен Гость Пт, 02/03/2012 - 12:38

Текст задачи составлен немного неправильно.
Необходима пометка, что первый математик рассказал ВСЁ, чтобы подобрать ЕДИНСТВЕННОЕ решение к задаче. Т.е. больше уточняющих вопросов от второго математика не нужно и задачу можно однозначно решить опираясь только на эти три условия! Необходима фраза от первого математика такого плана: "Я сказал тебе все условия, которых достаточно и при которых можно найти одно единственно верное решение!"

Тогда да, если опираться на то, что условий больше не нужно, и при этом существует одно единственное решение - то получаем: 1, 5 и 8 лет (согласно вышеописанной логике в ответе)

Но если мы не знаем, что трёх вышеуказанных условий нам достаточно, то получаем кучу вариантов и можем смело говорить: "Все еще не понимаю". Потому как второй математик после третьего вопроса всё ещё имеет кучу вариантов ( 2/4/6 и т.п.). И ответ о том, что средний сын любит танцевать, сам по себе не сужает круг вариантов! Так можно кучу предложений дальше говорить: "Мой младший сын любит рисовать!", "Мой старший сын катается на велосипеде" и т.д.

А так, задача сводится к банальному:
есть x,y,z

1) 6 2) 6* 3) x 4) условий достаточно
При этих условиях существует единственное решение, найдите его!

* практический начальный возраст 6 лет это конечно бред, но теоретически отвергать нельзя (мало ли - математик-вундеркинд и детям 1,2 и 3 года)
** пенсионный возраст 60 лет - тоже за уши притянуто, поскольку не оговаривается в какой именно стране и в какой временной период происходит действие

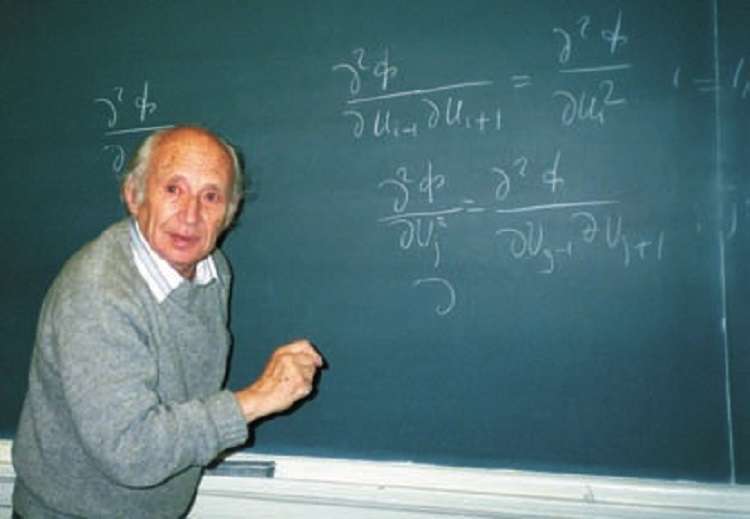
Израиль Гельфанд (1913-2009) — один из величайших математиков XX века, автор множества теоретических работ и прикладных исследований с применением математического метода в области физики, сейсмологии, биологии, нейрофизиологии, медицины. Родился в украинской деревне Окны. Окончив всего девять классов школы, не получив высшее образование, поступил в аспирантуру механико-математического факультета МГУ им. М.В. Ломоносова и уже в двадцать семь лет стал доктором наук, а в сорок — членом-корреспондентом Академии наук СССР.

Гельфанд — лауреат многочисленных отечественных и международных премий; почетный доктор семи иностранных университетов, включая Гарвард и Оксфорд; почетный иностранный член Американской академии искусств и наук.

Когда Израиль Гельфанд окончил девятый класс школы в небольшом местечке под Одессой, учитель математики сказал ему: «Изя, дорогой, я больше ничему тебя не смогу научить. Езжай в Москву, найди там МГУ, а в МГУ — мехмат. Учись дальше, и ты станешь великим математиком!»

На механико-математическом факультете МГУ девятиклассник дошел только до секретаря деканата.

— Молодой человек, где ваш диплом об окончании средней школы? — возмутился секретарь. — Ах, у вас его еще нет! Тогда езжайте к себе назад на Украину и приходите через год, с дипломом!

Но вернуться домой Гельфанд уже не мог — так запали в душу слова учителя о великом будущем. Он решил остаться в Москве, и чтобы заработать на жизнь, устроился гардеробщиком в Ленинскую библиотеку — все как-то ближе к книгам.

Однажды его заметил там за чтением монографии по высшей математике молодой, но уже знаменитый математик Андрей Николаевич Колмогоров.

Андрей Колмогоров (1903-1987) — советский математик, академик, почетный член нескольких западных академий наук, профессор МГУ им. М.В. Ломоносова, один из создателей современной теории вероятностей. Написал ряд важных работ по истории и философии математики. Был научным руководителем Израиля Гельфанда и не раз говорил про своего ученика: «Общаясь с Гельфандом, я ощущал присутствие высшего разума».

— Мальчик! Зачем ты держишь в руках эту книгу? — спросил ученый. — Ведь ты не понимаешь в ней ни строчки.

— Я извиняюсь, товарищ профессор, но вы не правы! — парировал Израиль.

— Не прав? Тогда вот тебе три задачки — попробуй решить хотя бы одну до моего возвращения. У тебя есть два часа!

Колмогоров пробыл в библиотеке дольше, чем рассчитывал, и, вернувшись за пальто, отдал номерок другому гардеробщику, совершенно забыв о поручении юному Гельфанду. Уже на выходе из вестибюля он услышал позади робкий оклик:

— Товарищ профессор! Я их решил…

Андрей Николаевич вернулся, взял у Гельфанда исписанные торопливым почерком листки, выдранные из школьной тетради, и с изумлением обнаружил, что все задачи решены, причем последняя, самая трудная — необычайно изящным и неизвестным ему способом.

— Тебе кто-то помог? — не мог поверить профессор.

— Я извиняюсь, но я решил все сам!

— Ты сделал это сам. Тогда вот тебе еще три задачки. Если решишь две из них, возьму на мехмат к себе в аспирантуру. У тебя на все про все четыре дня.

На пятые сутки Колмогоров появился в гардеробе Ленинки и направился прямиком к тому сектору, который обслуживал Израиль Гельфанд.

— Ну как дела? — полюбопытствовал профессор.

— Мне кажется, я их решил… — мальчик протянул математику листы с задачами.

Колмогоров погрузился в чтение. Изучив листки, ученый поднял голову, внимательно посмотрел Изе в глаза и сказал:

— Извините меня, пожалуйста, за сомнения в авторстве решений тех первых задач. Теперь я вижу, что вам никто не помогал. Дело в том, что ни в этой библиотеке, ни за ее пределами вам никто не мог подсказать решение нынешней третьей задачи: до сегодняшнего дня математики считали ее неразрешимой! Одевайтесь, я познакомлю вас с ректором МГУ.

Они застали ректора в его кабинете на Моховой. Тот сидел за столом, заваленным бумагами, и что-то напряженно писал. Ректор лишь мельком взглянул на вошедших:

— Андрей Николаевич! Мне надо срочно дописать документ, а вы врываетесь ко мне с каким-то мальчишкой!

— Простите великодушно, но это не мальчишка, а Израиль Моисеевич Гельфанд, гениальный математик, — уверенно представил Изю ректору первого университета страны Колмогоров. — Он любезно согласился пойти ко мне в аспирантуру. Прошу вас распорядиться.

Вот почему так случилось, что академик Гельфанд никогда не учился в 10-м классе и никогда не был студентом.

Новое видео:

Задачи для 5 — 8 класса.
Занимательная математика. Календарь, время, возраст

Задача №1. Пасмурные дни не любят туристы. Поможем группе туристов «ухватить» побольше солнечных дней.

На некотором острове необычайно регулярный климат: по понедельникам и средам всегда идут дожди,по субботам — туман, зато в остальные дни — солнечно.Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней?
( A ) в понедельник; (B) в среду; © в четверг; ( D ) в пятницу; ( E ) во вторник

Задача №2. Когда сравняются возраста ?

Матери 47 лет, троим ее сыновьям соответственно 10, 12, и 15 лет. Как скоро сумма возрастов сыновей сравняется с возрастом матери ?

Задача 3. Сколько лет сестре ?

Два года назад сестра была младше брата во столько раз, сколько лет было тогда брату.
Сколько лет сестре ?

Задача 4. Отец и сын

Отцу 36 лет, сыну 7 лет.
Через сколько лет отец будет вдвое старше сына?

Решение:↓
Способ 1. Когда отец станет вдвое старше сына, возраст сына сравняется с разностью их возрастов
(с одной стороны, возраст отца будет равен удвоенному возрасту сына, с другой стороны — возрасту сына плюс разность их возрастов).

Сын на 29 лет младше отца. 29 лет сыну исполнится через 22 года.

К этому времени отец достигнет возраста 36+22=58 лет и станет вдвое старше сына (58:2=29).

Способ 2. Разность между знаменателем и числителем дроби 7/36, выражающей отношение возраста сына к возрасту отца, составляет 29 и не меняется с течением времени.

Чтобы получить дробь, равную ½ и имеющую ту же разность 29 между знаменателем и числителем (т.е. привести дробь ½ к тому же масштабу, что и дробь 7/36, равному единице), нужно числитель и знаменатель дроби умножить на 29: ½=29/58.

Дробь 29/58 может быть получена из дроби 7/36 увеличением числителя и знаменателя ее на 22. Следовательно, через 22 года отец будет вдвое старше сына.

Способ 3. Когда родился сын, отцу было 29 лет. Когда отцу добавится 29 лет, он станет вдвое старше.

Сын, которому к этому времени исполнится 29 лет, окажется вдвое младше отца. Случится это через 22 года (29-7).

Задача 5. Брат и сестра

Два года назад брат был старше сестры в два раза,
а 8 лет назад – в 5 раз.
Сколько лет брату и сколько – сестре?

Решение:↓
Способ 1. Два года назад возраст сестры был равен разности возрастов брата и сестры;
восемь лет назад возраст сестры был в 4 раза меньше этой разности.

Значит, за 6 лет возраст сестры увеличился в 4 раза,

т.е. к ее первоначальному возрасту добавилось еще 3 ее возраста.

Отсюда следует, что 8 лет назад сестре было 6 : 3 = 2 года, сейчас ей 10 лет.

Брату 8 лет назад было 2 · 5 = 10 лет; сегодня ему 18 лет.

Способ 2. Два года назад возраст брата выражался четным числом (он был равен удвоенному возрасту сестры).

Очевидно, 8 лет назад возраст брата также выражался четным числом, а также, согласно условию, был кратен 5.

Следовательно, 8 лет назад возраст брата был кратен 10.

Проверкой убеждаемся, что 8 лет назад брату было 10 лет.

Проверку начинаем с минимального значения возраста,

поскольку столь существенные изменения соотношения возрастов могут иметь место лишь в области малых значений искомых величин.

Способ 3. Отношение возраста сестры к возрасту брата два года назад — 1 : 2,
8 лет назад — 1 : 5.

Разность возрастов брата и сестры с течением времени не меняется.

Преобразуем дроби, выражающие отношение их возрастов в разные моменты времени так, чтобы обеспечить равные разности знаменателей и числителей в обеих дробях.

В дроби ½ знаменатель на 1 больше числителя, в дроби 1/5 — на 4.

Умножим числитель и знаменатель дроби ½ на 4: ½ = 4/8.

Рассмотрим дроби 1/5 и 4/8, выражающие отношения возрастов сестры и брата в разные моменты времени в одном и том же масштабе (иными словами, исходные дроби сокращены на одну и ту же величину).

Числитель второй дроби больше числителя первой на 3, такова же разность знаменателей двух дробей.

На самом же деле интервал времени между двумя рассматриваемыми моментами — 6 лет,

т.е. вдвое больше указанной разности.

Умножим числители и знаменатели полученных дробей на 2.

1/5 = 2/10, 4/8 = 8/16. Числители, равно как и знаменатели полученных дробей разнятся на 6 и представляют соответственно возрасты сестры и брата в рассматриваемые моменты:

первая дробь — отношение восьмилетней давности, вторая — двухлетней.

Два года назад сестре было 8 лет, брату — 16; ныне им соответственно 10 и 18 лет.

Задача 6. Когда был перерыв?

У моего друга трое часов в квартире:
аналоговые (со стрелками) механические часы, которые всегда показывают правильное время;
аналоговые электрические часы;
электрические цифровые часы.
Когда нет света в квартире, аналоговые электрические часы останавливаются. Но когда электричество возвращается, эти часы начинают отсчитывать время от той точки, когда они остановились.

Экран цифровых электрических часов, когда нет света, гаснет. Однако, когда электричество возвращается, экран начинает мигать, часы начинают отсчет времени с 12:00.

Однажды утром мой друг ушел на работу, когда все его часы показывали 6:30. Возвратившись вечером домой, он обнаружил:

его механические часы показывают 8:21;
аналоговые электрические часы показывают 7:50,
а цифровые электрические показывают 6:03, мигая.
Предположим, что был только один перерыв в подаче энергии, когда он начался и когда закончился?
Два школьника прислали интересные решения. Оба исходили из того, что механические часы никак не пострадали от сбоя эл. энергии и показывают правильное время возвращения друга, т.е. 8 часов и 21 минута.

Решение:↓
Вариант №1 семиклассника Мартыненко Николая из г. Саратова:

«Сначала определим, сколько продолжался перерыв. Во время перерыва аналоговые электрические часы останавливаются, но время не сбрасывается.

Значит перерыв продолжался 8 ч 21 мин – 7 ч 50 мин = 31 мин.

Далее определим, когда перерыв закончился. С того момента цифровые электрические часы отсчитали 6 ч 03 мин.

Значит, перерыв закончился в 8 ч 21 мин – 6 ч 03 мин = 2 ч 18 мин.

Соответственно, перерыв начался в 2 ч 18 мин – 31 мин = 1 ч 47 мин»

Вариант №2 семиклассника Канафеева Рустама, ученика 7 класса (Кротовка):

«Так как цифровые часы начинают отсчет времени с 12:00, то перерыв закончился 6:03 назад, т.е. 8:21 — 6:03 = 2:18.

Электрические часы начинают отсчет с той точки , когда они остановились, они включились 6:03 назад, тогда перерыв начался 7:50 — 6:03 = 1:47.

Итак, перерыв начался в 1:47 и закончился в 2:18.»

Читайте также: